public double sin(double angle, String type)
{
double length = 0, x;
if(type == "deg") //Change to radians if not already
{
angle = (angle/180)*(Math.PI);
}
x = angle; // x is easier to work with than a word
while(x > Math.PI) //Bring x into the accurately represented range.
{
x = x-(2*Math.PI);
}
while(x < -Math.PI)
{
x = x+(2*Math.PI);
}
//The polinomial calculation
length = (x-(Math.pow(x, 3)/6)+(Math.pow(x, 5)/120)-(Math.pow(x, 7)/5040)+(Math.pow(x, 9)/(362880))-(Math.pow(x, 11)/39916800));
return length;
}
This is where maths and technology come together beautifully. You see, a computer is a very stupid thing, literally the only piece of maths it can do at it's most basic level is add. Luckily maths at its most basic level is also just adding. So to do other maths functions we need to add in a certain way a certain number of times. For example subtraction is just adding a negative number, multiplication is just adding a number several times. You get the idea. However trigonometry functions(sin, cos, tan etc) are different, they cannot be calculated using addition alone so they pose a serious problem to computers. This is where maths comes to the rescue. In the area of sequences and series there is a special kind of series called a Maclaurin series, I won't bore you with how it's calculated but the great thing about them is that they can be used to model other functions in maths, like sin, with only the use of adding! Here's the formula for them:
f(x) = f(0)+ f '(0)*x + f "(0)* x^2/2!+ f "'(0)*x^3/3!+...+ f(n)(0)*x^n/n!+....
I say "model" because this formula is almost never totally precise but it's pretty good. If you were to work out this formula to infinite terms ie: n = ∞, then you would get an exact answer but we don't have enough time to do that, not even with a very very fast computer. It's alright to stop calculating at about the fifteenth term because the number you calculate would be accurate to about the tenth decimal place which is plenty for most applications. So when you do a trig function on your calculator it's not actually giving you back the trig function, just something very much like it.
When you actually implement a piece of code to calculate sin you have to handle the input number being greater than PI or less than -PI because sin goes for ever to infinity and to negative infinity and the pattern repeats every 2PI. The polynomial which is the Maclaurin series only accurately models sin from about -PI to PI which means if the input number passed into the method is grater than Pi you have to subtract 2PI from it over and over again until the number is within the accurate range. Or if it's less that -PI, you must add 2PI onto it until it's within range. Doing this doesn't change the output number because the value at any one point is equal to the value at that point +/- 2PI. It's a repeating pattern.
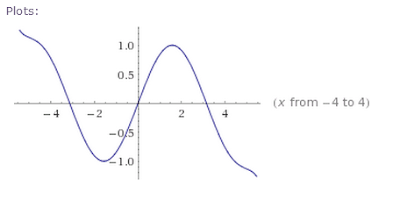
This is what y = sin(x) looks like.
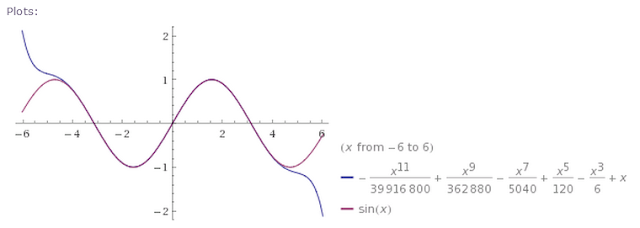
This is what the Maclaurin series representation of y = sin(x) looks like.
And this is them laid on top of one another. As you can see, they're basically identical from about - 4 to 4.
